reglas de la multiplicación

Regla de multiplicación de probabilidades

Regla de multiplicación de probabilidades

1. Regla de multiplicación de probabilidades

Si se tienen varios eventos sucesivos e independientes entre sí, la probabilidad de que ocurran todos ellos a la vez corresponde a la multiplicación de las probabilidades de cada uno de los eventos.

Ejemplos:
1. Si se responden al azar cuatro preguntas con cinco opciones cada una, ¿cuál es la probabilidad de acertar a todas?

La probabilidad de acierto en cada una de las preguntas es 1/5. Por lo tanto, la probabilidad de acertar en las cuatro es:

 

2. Suponiendo que la probabilidad de tener un hijo o una hija es ½, ¿cuál es la probabilidad de que al tener tres hijos, 2 solamente sean varones?

Si H representa el nacimiento de un hombre y M el de una mujer, tenemos los siguientes casos favorables:    HHM – HMH – MHH 
La probabilidad de cada uno de estos eventos es: 

De la definición de probabilidad condicional se tienen los siguientes resultados al despejar 

Las relaciones  y  son casos especiales de la llamada Regla de la multiplicación, la cual es útil para:

Calcular probabilidades de intersecciones de eventos con base en probabilidades condicionales.

Esta regla de manera general se puede expresar como:

Sea  eventos tales que . Entonces

Ejemplo

1. (Inspección de Lotes)

Un lote contiene  items de los cuales  son defectuosos. Los items son seleccionados uno despues del otro para ver si ellos son defectuosos. Suponga que dos items son seleccionados sin reemplazamiento(Significa que el objeto que se selecciona al azar se deja por fuera del lote). ¿ Cúal es la probabilidad de que los dos items seleccionados sean defectuosos?.

Solución

Sea los eventos

entonces dos items seleccionados seran defectuosos, cuando ocurre el evento  que es la intersección entre los eventos  y . De la información dada se tiene que:

 

así probabilidad de que los dos items seleccionados sean defectuosos es

Ahora suponga que selecciona un tercer item, entonces la probabilidad de que los tres items seleccionados sean defectuosos es

PROBABILIDAD

Es una medida númerica de la posibilidad de que ocurra un evento. Las medidas de la probabilidad siempre se asignan de 0 a 1. Una probabilidad cerca a 0 indica que es poco probable que ocurra un evento y una probabilidad cerca de 1 indica de que es casi seguro de que ocurra el evento.

EXPERIMENTO Cualquier proceso que genere resultados bien definidos. ESPACIO MUESTRAL Conjunto de todos los puntos muestrales. Es decir el conjunto de todos los resultados posibles para el mismo. PUNTO MUESTRAL Es un resultado experimental y también un elemento del espacio muestral.

EJEMPLO

En un proceso de control de calidad, el inspector selecciona una pieza terminada para inspección. El inspector a continuación determina si la pieza tiene algún defecto importante, un defecto menor o no tiene defectos. Considere la selección y clasificación de la pieza como un experimento. Enliste los puntos muestrales o eventos simples para el experimento. RESPUESTA Los puntos muestrales o eventos simples son: No efecto importante Un defecto menor No tiene defectos.

EJEMPLO Experimento: Lanzar un dado Resultados Experimentales: 1,2,3,4,5,y 6 Espacio muestral: S { 1,2,3,4,5,6}

MÉTODO CLÁSICO

Es cuando se usa la suposicion de resultados igualmente probables como una base para asignar probabilidades . Si un experimento tiene n resultados posibles el metodo clasico asigna una probabilidad de 1/n a cada resultado experimental. El metodo clasico fue elaborado para analizar probabilidades en los juegos de azar donde la suposicion de resultados igualmete probables frecuente es razonables. Probabilidad 1/6 = 0.1666 la probabilidad de obtener un número particular en el lanzamiento de un dado es 0.1666

METODO SUBJETIVO

Es utilizado para asignar probabilidades apropiando cuando no supone de manera realista que todo resultado experimentales son iguales probables y cuando se dispone de pocos datos relevantes. Ejemplo: Al comprar una casa se hace una oferta: Dos posibilidades : La oferta es aceptada ó la oferta es rechazada

COMPLEMENTO DEL EVENTO A

El evento que contiene todos los puntos muestrales, no existentes en A.

DIAGRAMA DE VENN

Dispositivo gráfico para representar el espacio muestra y las operaciones que involucran eventos.

INTERSECCIÓN DE EVENTOS A y B

El evento que contiene todos los puntos muestrales existentes, tanto en A como en B.

UNIÓN DE EVENTO A y B

El evento que contiene todos los puntos muestrales existentes en A, en B, o en ambos.

LEY DE LA ADICIÓN

Una ley de probabilidades utilizada para calcular la probabilidad de una unión: P(A ² B) = P(A) + P(B) – P(A ³ B). Para eventos mutuamente exclusivos, P(A ³ B) = 0 y se reduce a P(A U B) = P(A) + P(B).

EJEMPLO

Hay 15 clínicas en una ciudad. De ellas, 6 no cumplen las reglas sanitarias y 8 no cumplen los requisitos de seguridad. 5 clínicas no cumplen ni los requisitos de seguridad ni las reglas sanitarias. Si se elige una clínica para inspeccionar al azar, ¿cual es la probabilidad de que cumpla ambos reglamentos? SOLUCIÓN Sea A el suceso de que cumple las reglas sanitarias y B el suceso de que cumple los requisitos de seguridad. Si elegimos una clínica al azar, tenemos P(A) = 6/15 P(B) = 8/15 P( A y B) =5/15 Deducimos que P(A) = P(A) = 9/15 y también que P(B) = 7/15. (A o B)y(A y B) = ? Luego P(A o B) = P(AyB) = 10/15 Calcular P(A y B). P(A o B) = P(A)+P(B); P(A y B) P(A y B) = 9/15 + 7/15 *10/15 = 6/15 = 2/5

EVENTOS MUTUAMENTE EXCLUYENTES

Eventos que no tienen ningún punto muestral en común; esto es: A ³ B está vacío y P(A ³ B) = O.

PROBABILIDAD CONJUNTA

La probabilidad de la intersección de dos eventos.

TABLA DE PROBABILIDADES CONJUNTAS

Tabla utilizada para mostrar probabilidades conjuntas y marginales.

PROBABILIDAD MARGINALES

Los valores en los márgenes de la tabla de probabilidades conjuntas, que proporcionan la probabilidad de cada evento por separado. Eventos dependientes Dos eventos A y B, donde P(A I B) ; P(A) o P(B I A) ; (B); esto es, la probabilidad de que un evento sea alterado o afectado al saberse que ocurre otro evento.

EVENTOS INDEPENDIENTES

Dos eventos A y B donde P(A I B) = P(A) y P(B I A) = P(B); esto es, eventos que no tienen influencia uno sobre otro.

LEY DE LA MULTIPLICACIÓN

Una ley de probabilidad utilizada para calcular la probabilidad de una intersección: P(A y B) = P(A|B)P(B). EJEMPLO Se dan dos cartas de una baraja española. ¿Cuál es la probabilidad de que ambas cartas sean copas? Sea A (B) el suceso de que la primera (segunda) carta sea copa. se quiere P(A y B). SOLUCIÓN Ahora P(A) = 10 /40 y P(B|A) = 9/39 porque si la primera carta es copa, quedan 39 cartas, nueve de ellos siendo copas. Luego P(A y B) = (10/40)× (9/39) = 3/52

PROBABILIDADES PREVIAS

Probabilidades iniciales de eventos.

PROBABILIDADES POSTERIORES

Probabilidades de eventos revisadas con base en información adicional.

PROBABILIDAD CONDICIONAL

Probabilidad de que ocurra un evento dado que ha ocurrido otro evento. La probabilidad condicional de A DADO P(A/B) = P(A n B) / P(B) EJEMPLO Durante el mes cero cierto producto es preferido por el 60% del mercado y otros varios por el resto. Los clientes compran una vez al mes . Si alguien compra el producto A, la probabilidad que lo vuelva a comprar en el siguiente mes es de 75% y de un 25% de que se cambie. Si un cliente compra un producto de la competencia en un mes la probabilidad que se cambie al producto A es de 45% y 55% de que permanezca fiel a la marca de la competencia. Encuentre el porcentaje de participación esperado en el mercado por A al final del segundo mes. SOLUCION: Aquí realizaremos un diagrama de árbol donde definiremos primero la probabilidad de aceptación en el primer mes por el producto A que en este caso seria el 60%, y el 40% seria el del producto de la competencia. Para sacar las probabilidades del segundo mes primero debemos de hacerlo para el producto A donde del 60% que compran aquí el 75% sigue comprando este producto y el 25% se cambia al otro producto. Para los que en el primer mes compraron el producto de la competencia que era el 40% , en el segundo mes que compraron el 45% se cambio al producto A y el 55% siempre compró el producto de la competencia , tomando encuentra que el porcentaje es igual a la probabilidad de cada uno por lo que nuestro diagrama del árbol quedaría de esta forma:

En este caso solo nos interesa que en el segundo mes o sea al final los clientes compren el producto A, esto quiere decir, que solo vamos a tomar encuentra los porcentajes de aceptación del producto A, ya sea que desde el inicio compro el producto A o no pero que al final si compro A. Por lo que nos quedaría de esta forma: P( C ) = ( 0.6*0.75) + (0.4*0.45) = 0.63 Donde el primer paréntesis representa que al inicio prefiere A y luego permanece en A, y el segundo paréntesis representa que al inicio prefiere B pero que luego al final prefiere A. Obteniendo así las 2 formas donde terminan comprando al final el producto A. También se puede hacer de la siguiente forma: P( C ) = (A 1 A 2 ) U (B 1 A 2 ) P( C ) = P(A 1 )* P(A 2 /A 1 )+ P(B 1 )* P(A 2 /B 1) En donde: P(A)= 0.6 P(B)= 0.4 P(A 2 /A 1 ) = 0.75 P(B 2 /A 1 )= 0.25 P(B 2 /B 1 )= 0.55 P(A 2 /B 1 )= 0.45 Por lo que nos quedaría de la siguiente forma: P( C ) =(0.6)* (0.75)+ (0.4)* ( 0.45) =0.63

TEOREMA DE BAYES

Método utilizado para calcular probabilidades posteriores.

Las probabilidades p(A1) se denominan probabilidades a priori. Las probabilidades p(Ai/B) se denominan probabilidades a posteriori. Las probabilidades p(B/Ai) se denominan verosimilitudes. EJEMPLO El 20% de los empleados de una empresa son ingenieros y otro 20% son economistas. El 75% de los ingenieros ocupan un puesto directivo y el 50% de los economistas también, mientras que los no ingenieros y los no economistas solamente el 20% ocupa un puesto directivo. ¿Cuál es la probabilidad de que un empleado directivo elegido al azar sea ingeniero?

La probabilidad de que haya un accidente en una fábrica que dispone de alarma es 0.1. La probabilidad de que suene esta sí se ha producido algún incidente es de 0.97 y la probabilidad de que suene si no ha sucedido ningún incidente es 0.02. En el supuesto de que haya funcionado la alarma, ¿cuál es la probabilidad de que no haya habido ningún incidente? Sean los sucesos: I = Producirse incidente. A = Sonar la alarma.

Regla general para eventos dependientes

Si A y B son dos eventos dependientes, es decir, si la ocurrencia de A afecta la probabilidad de ocurrencia de B, entonces, dicha probabilidad de calcula empleando la siguiente regla:

Nota:

La probabilidad del evento B, calculada bajo la suposición de que el evento A ha ocurrido, se denomina probabilidad condicional de B, dado A, y se denota por P (B/A).

Ejemplos ilustrativos

1) De una baraja estándar de 52 cartas sea A el suceso de sacar un As en la primera extracción y B sacar un As en la segunda extracción. Calcular la probabilidad de sacar dos Ases en dos extracciones sin devolver la carta extraída.

Solución:

A y B son sucesos dependientes porque la ocurrencia de A afecta la probabilidad de ocurrencia de B.

La probabilidad de que la primera carta sea un As es:

Reemplazando los anteriores valores en la regla general de la multiplicación de probabilidades para eventos dependientes se obtiene:

2) Sea A el suceso de sacar un As de una baraja estándar de 52 cartas y B sacar un Rey de corazón rojo. Calcular la probabilidad de sacar un As y un Rey de corazón rojo en dos extracciones sin devolver la carta extraída.

Solución:

A y B son sucesos dependientes porque la ocurrencia de A afecta la probabilidad de ocurrencia de B.

La probabilidad de que la primera carta sea un As es:

Reemplazando los anteriores valores en la regla general de la multiplicación de probabilidades para eventos dependientes se obtiene:

3) En una clase de 50 alumnos, 10 alumnos tienen como preferencia solamente la asignatura de Matemática, 15 prefieren solamente Estadística y 5 no tienen preferencia por ninguna de estas asignaturas. Calcular la probabilidad que de un alumno de la clase seleccionado al azar tenga preferencia por

4.1) Matemática y Estadística.

4.2) Estadística y Matemática

Solución:

Realizando un diagrama de Venn-Euler se obtiene:

Simbología:

S = espacio muestral

A= Matemática

B = Estadística

a = Solamente Matemática

b = Solamente Estadística

c = Matemática y Estadística

d = Ninguna de las dos asignaturas

Datos y cálculos:

a = 10

b = 15

c = S - a - b - d = 50 - 10 - 15 - 5 = 20

d = 5

S = 50

4.1) Matemática y Estadística.

O también, observando el diagrama de Venn-Euler se tiene directamente la probabilidad solicitada:

La suposición de que el alumno seleccionado tenga preferencia por Matemática significa que sólo consideremos el conjunto A, de los 30 elementos de A, sólo 20 tienen preferencia por Estadística. Por lo tanto la probabilidad condicional P(B/A) = 20/30 = 2/3

O también, observando el diagrama de Venn-Euler y aplicando la fórmula de la probabilidad condicional se tiene:

Reemplazando valores en la regla de la multiplicación para eventos dependientes se obtiene:

4.2) Estadística y Matemática.

O también observando el diagrama de Venn-Euler se tiene directamente la probabilidad solicitada:

La suposición de que el alumno seleccionado tenga preferencia por Estadística significa que sólo consideremos el conjunto B, de los 35 elementos de B, sólo 20 tienen preferencia por Matemática. Por lo tanto la probabilidad condicional P(A/B) = 20/35 = 4/7

Reemplazando valores en la regla general de la multiplicación:

Los cálculos en Excel se muestran en la siguiente figura:

Notas:

En los eventos dependientes se cumple:

4) De una tómbola que contiene 3 bolas rojas y 5 blancas, Mathías extrae tres bolas, sin volver a la tómbola la bola extraída, calcular la probabilidad de que las 3 bolas extraídas sean:

6.1) Rojas

6.2) 2 rojas y una blanca

6.3) Una roja y 2 blancas

6.4) 3 blancas

Solución:

6.1) Rojas

En 3 sucesos la fórmula de la regla general de probabilidades es:

Reemplazando valores en la regla general de de la multiplicación se obtiene:

O también, elaborando un diagrama de árbol se tiene todas las probabilidades:

En el diagrama de árbol, la probabilidad correspondiente a cada rama del árbol corresponde a la probabilidad condicional de que ocurra el evento específico, dado que han ocurrido los eventos de las ramas precedentes. Al describir un evento mediante una trayectoria a través del diagrama de árbol, la probabilidad de que ocurra dicho evento es igual a producto de las probabilidades de las ramas que forman la trayectoria que representa al mencionado evento.

La solución empleando el diagrama de árbol para  es multiplicando las ramas RRR, es decir,

Los cálculos en Excel se muestran en la siguiente figura:

Regla particular o especial para eventos independientes

Si A y B son dos eventos independientes, es decir, si el conocimiento de la incidencia de uno de ellos no tiene efecto en la probabilidad de ocurrencia del otro, entonces, para calcular la probabilidad de dichos eventos se aplica la siguiente regla:

Nota: Dos eventos A y B son independientes si la ocurrencia de uno de ellos no afecta la probabilidad de ocurrencia del otro, esto es, si 

Ejemplos ilustrativos

1) De una baraja estándar de 52 cartas sea A el suceso de sacar un As en la primera extracción y B sacar un Rey en la segunda extracción. Calcular la probabilidad de sacar un As y un Rey en dos extracciones devolviendo la carta extraída.

Solución:

A y B son sucesos independientes porque la ocurrencia de A afecta la probabilidad de ocurrencia de B.

La probabilidad de que la primera carta sea un As es:

Reemplazando los anteriores valores en la regla particular de la multiplicación se obtiene:

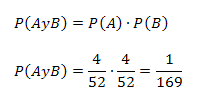
2) Una pareja de esposos desean tener 3 hijos. Suponiendo que las probabilidades de tener un niño o una niña son iguales, calcular la probabilidad de éxito en tener hombre en el primer nacimiento, mujer en el segundo nacimiento y hombre en el tercer nacimiento.

Solución:

M = mujer

H = hombre

Elaborando un diagrama de árbol se tiene todas las probabilidades:

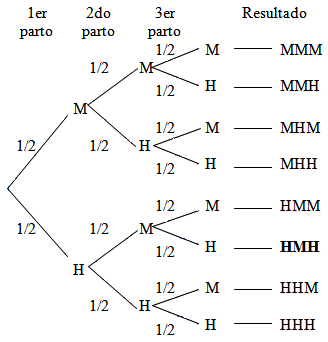
Entonces,